Uno escucha frecuentemente a científicos y divulgadores hablar sobre la entropía, a veces quizás de una manera misteriosa. ¿Qué es esta cosa que siempre aumenta? ¿Qué tiene que ver con mi habitación desordenada (spoilers: nada)?
En este artículo no llegaremos a explicar todo, de momento vamos a dar una definición de la entropía enfocada desde el punto de vista de la información. Después en artículos futuros lo enlazaremos con la física estadística y la termodinámica llegando a cubrir la segunda ley también.
Supongamos que tenemos un sistema y buscamos estudiarlo. Partamos primero de un ejemplo sencillo (ya después generalizaremos) para introducir los conceptos básicos de la probabilidad, que son esenciales para todo lo demás. Después iremos introduciendo conceptos elementales de la teoría de la información culminando con la entropía.
Como ejemplo, digamos que tenemos una rata en una caja y dividimos el suelo en 9 zonas iguales (como en el Tic-Tac-Toe). Al mirar la caja apuntamos el cuadro en el cual se encuentra la rata. Si repetimos esto muchísimas veces (siempre en las mismas condiciones) podemos hallar la fracción de veces que la hemos encontrado en cada cuadro, y conforme el número de repeticiones aumenta esta fracción tenderá a un valor que llamamos probabilidad (esta es la visión frecuentista). Notemos que en lugar de representar las probabilidades en tanto por ciento (es decir, que todas las probabilidades sumen 100), lo haremos en tanto por uno porque es lo usual en matemáticas.
Otro enfoque válido es el bayesiano, que es el que consideraremos durante el resto del artículo. Supongamos que buscamos predecir lo que vamos a medir sin realizar ninguna medida anteriormente (muchas veces no es posible medir para calcular la distribución). Entonces podemos asignar una probabilidad nosotros a cada celda en función de lo que sabemos sobre su posición. Si estamos completamente seguros de conocer la celda en la cual se localiza, entonces asignamos $latex p=1$ a dicha celda y $latex p=0$ a todas las demás (vamos a llamar a esta distribución «delta» para darle un nombre). En el caso opuesto, si no conocemos nada, si nuestra incertidumbre es máxima, asignaríamos la misma a todas (distribución plana), en este caso $latex p=\frac{1}{9}$ para que la suma de las nueve sea 1.
Con este ejemplo espero que vean plausible que hay una estrecha relación entre la distribución de probabilidad y la información. La idea de información es interesante, pero a la vez no muy clara. ¿Cómo podríamos definirla matemáticamente sin perder nuestra intuición? Una buena idea es evitar el lío de cuantificarla en modo absoluto y simplemente dar las diferencias en contenido de información (información relativa), es decir, cuanta información tiene o le falta a una distribución con respecto a otra.
El convenio es utilizar la distribución delta como referencia (la de máxima información). En este caso la diferencia se puede interpretar como desinformación, porque nos diría la información que le falta a una distribución cualquiera para llegar a ser la de máximo conocimiento (o en otras palabras, si tenemos una distribución sobre distintas posibilidades mutuamente excluyentes, la desinformación nos dice cuanta información ganaríamos si de repente se nos revelara cual es el estado real del sistema). Cuanta mayor es la desinformación, mayor es la incertidumbre (en la distribución delta estamos siempre seguros de lo que saldrá pero la plana es la más impredecible y la que más nos sorprende).
Conviene introducir ahora algunas definiciones de la teoría de probabilidad y generalizar un poco para simplificarnos la vida. Vamos a llamar espacio muestral $latex S$ al conjunto de todos los posibles estados, $latex n$ en número, del sistema (en nuestro ejemplo tenemos 9 posibles resultados al medir la posición). Un evento $latex A$ es un subconjunto del espacio muestral, es decir, un conjunto de posibles estados (un ejemplo sería el evento de que la rata se encontrase en alguna de las cuatro esquinas; la probabilidad de este evento es la suma de las probabilidades de las esquinas).
Denotaremos a la distribución de probabilidad como $latex p(i)$, significando la probabilidad del estado $latex i$-ésimo. Naturalmente, se debe cumplir que $latex \sum_{i=1}^{n}p(i)=1$. Vamos a llamar variable aleatoria a una función que nos devuelve el resultado de una medida pero siguiendo ciertas probabilidades (en el caso de la rata, su posición es la variable aleatoria).
Ahora, hay distintas formas de representar las distribuciones. La más sencilla es mediante una gráfica, como se puede ver a continuación:

Nótese que la suma de todas las probabilidades es 1.
Otra forma útil es representar las probabilidades mediante áreas. Cogemos una región sin agujeros y decimos que su área es 1. A esta región la dividimos en subregiones que representan eventos y cuyas áreas son proporcionales a la probabilidad del evento. Un ejemplo de esto último sería un diagrama de Venn:
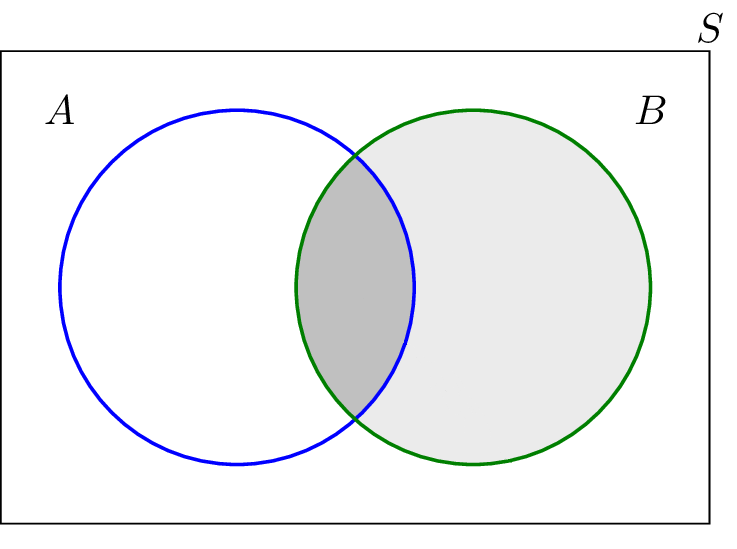
En este caso los dos eventos, A y B, tienen la misma área luego la misma probabilidad. El espacio muestral sería el rectángulo S de área 1.
Estas distintas representaciones no las introducimos por mera curiosidad, sino que resultan útiles para entender las ideas que intentamos transmitir.
Volviendo al hilo anterior, dijimos que vamos a medir la información relativa de una distribución respecto a la que intuitivamente debería tener «máxima información» (la distribución delta). ¿Cómo haremos esto? Lo más cómodo es inspirarnos en la realidad: nosotros ganamos información realizando preguntas.
Volvamos al ejemplo del principio: tenemos una distribución de probabilidad de encontrar la rata en una cierta posición (esta distribución refleja nuestro conocimiento del sistema de alguna manera). Ahora podemos preguntar cosas como, por ejemplo, «¿se encuentra la rata en la posición 2 ó 5 ó 6 (sean las que sean estas)?» Recibiremos un “SÍ” con una cierta probabilidad y un “NO” con otra, luego en lenguaje matemático una pregunta es una variable aleatoria, en este caso de dos posibles respuestas.
Observemos que al realizar esta pregunta hemos dividido el espacio muestral en dos eventos: que se encuentre en 2 ó 5 ó 6 (evento $latex A$) o que no se encuentre (evento $latex B$). Las probabilidades de estos eventos dependen naturalmente de la propia distribución porque $latex p(A)=p(2)+p(5)+p(6)$ y $latex p(B)=1-p(A)$. En general no serán iguales, pero podemos apañarlas para que lo sean porque al formular la pregunta nosotros elegimos en qué dos eventos partir el sistema, luego podemos escogerlos tal que $latex p(A)\approx p(B)$. Cuando hay pocos estados esto es difícil, pero si pensamos en sistemas con 7 000 000 de posibilidades y cada una con su probabilidad, entonces es razonable pensar que podemos encontrar dos eventos con probabilidades bastante iguales.
Entonces, suponiendo que realizamos las preguntas de esta forma, notemos que una vez recibida una respuesta, nosotros tenemos que actualizar nuestra distribución de probabilidad para tener en cuenta la nueva información. Si por ejemplo la rata NO se encuentra en 2 ó 5 ó 6 entonces hacemos $latex 0=p(2)=p(5)=p(6)$ y normalizamos las probabilidades restantes (hacemos tal que sumen 1). Una vez hecho esto, volvemos a preguntar algo similar como por ejemplo, “¿está en 7 ó 8?” En función de la respuesta actualizamos otra vez la distribución. Hacemos esto hasta que una de las respuestas nos diga exactamente en qué posición se encuentra la rata. Ahora, con la última actualización se ha llegado a la distribución delta (hemos ido anulando la probabilidad de algún estado con cada actualización hasta que nos ha quedado todo nulo menos uno: la posición real).
Fijémonos en lo que hemos hecho: mediante pasos sucesivos realizando preguntas hemos transformado nuestra distribución genérica $latex p(i)$ en una distribución delta. Si cada pregunta representa un aumento en información, entonces podemos escoger el número de preguntas que realizamos como una medida de este aumento. Tenemos el problemilla de que este número de preguntas es una variable aleatoria: algunas veces haremos más y algunas menos. Entonces, podemos arreglar esto cogiendo el promedio de preguntas.
Todo esto es bastante abstracto, luego si el lector se ha perdido, ¡le viene al rescate un ejemplo visual! Cojamos un sistema con 16 posibilidades y supongamos que todas las probabilidades son iguales (distribución plana). En la siguiente imagen imagínese que el cuadrado grande (que es el espacio muestral S) está dividido en 16 cuadrados iguales al cian (no se han dibujado todos para facilitar la lectura). Digamos que el sistema está en el estado $latex i$, con probabilidad $latex p_i$.

Siguiendo los principios anteriores, dividimos $latex S$ en dos mitades (eventos de igual probabilidad) y preguntamos al sistema en cual está. La respuesta es «mitad derecha» (descartamos el rectángulo «1» en el dibujo). Ahora dividimos la mitad derecha en dos y preguntamos si el sistema está en la mitad superior o inferior. La respuesta es «superior» (descartamos la región «2»). Ahora lo mismo otra vez y la respuesta es «mitad inferior» (descartamos «3»). Por último preguntamos si es la izquierda o derecha y la respuesta es «izquierda» (descartamos «4»).
Con cada pregunta dividimos $latex S$ en dos hasta que el área es igual a $latex p_i$. Si en general hacemos $latex N$ preguntas, entonces se tiene
$latex \frac{1}{2^N} \approx p(i) \rightarrow N \approx \log_2 \frac{1}{p(i)}$
El promedio del número de preguntas binarias de este tipo es lo que definimos como desinformación $latex H$:
$latex H = \sum_{i=1}^n p(i)\log_2 \frac{1}{p(i)}&s=1$
También se llama entropía de Shannon. Lo mismo dicho en otras palabras sería que la entropía nos dice en promedio cuantos bits necesitamos para almacenar el estado completo de un sistema. Si en lugar de preguntas binarias hiciésemos preguntas ternarias o de algún otro número de respuestas lo único que cambiaría es la base del logaritmo; las distintas entropías serían iguales salvo un factor multiplicativo. De hecho usualmente se usa el logaritmo en base $latex e$ por comodidad aunque no haya preguntas con 2.71… respuestas (las unidades se llaman nats a diferencia de los bits de las binarias).
El lector puede comprobar que la entropía de la distribución plana ($latex p(i)=\frac{1}{n}$) es $latex H=\log n$ y que la entropía de la distribución delta es cero (se debe definir $latex 0\cdot \log 0=0$; la justificación está en que el límite de $latex x\log x$ para $latex x\to 0$ es cero).
Ahora, después de aguantar tanto trabajo, ¿dónde está la física? En un futuro llegaremos desde la entropía de Shannon a la entropía de Boltzmann, que es el logaritmo del número de estados microscópicos de un sistema termodinámico compatibles con unas medidas macroscópicas.
Si te ha gustado el artículo o crees que ha sido una basura o tienes cualquier pregunta, tienes a tu disposición la sección de comentarios, ¡quiero escuchar tu opinión!
Apéndice – Discusión y comentarios
En este apéndice comento algunos aspectos que no he incluido en el texto principal porque demasiados detalles dificultan la lectura.
Un asunto muy relevante es que el rigor es imprescindible si se quieren hacer las cosas bien. Quiero dejar claro que este no ha sido el desarollo histórico de estas ideas ni es como se suelen presentar en cursos serios de mecánica estadística. La manera de hacerlo bien es motivar algunas propiedades de la entropía que parecen razonables y ver matemáticamente que llegamos a la misma definición de entropía. Dichas propiedades son:
- $latex H$ es una función continua de $latex p(i)$. La idea de esto es que las entropías de dos distribuciones muy próximas entre sí también son próximas.
- Si $latex p(1)=p(2)=\cdots=p(n)=\frac{1}{n}$ entonces $latex H(p(i))$ es máxima (lo que dijimos de que la distribución plana es la de mínima información).
- Supongamos que tenemos $latex p(1)=\frac{1}{2}$, $latex p(2)=\frac{1}{3}$ y $latex p(3)=\frac{1}{6}$ (suman 1). Ahora, porque nos da la gana, podríamos en lugar de dar tres posibilidades dar dos: $latex p(1)=\frac{1}{2}$, $latex p(2\,o\,3)=\frac{1}{2}$. Ahora, suponiendo que estamos en 2 o 3, tenemos $latex p(2\,\text{dado que estamos en 2 o 3})=\frac{2}{3}$ y $latex p(3\,\text{dado que estamos en 2 o 3})=\frac{1}{3}$ (lo único que hemos hecho es renormalizar las probabilidades de antes dividiéndolas entre $latex \frac{1}{3}+\frac{1}{6}$). La idea ahora es que la entropía no debería depender de una elección tan arbitraria, luego la de la distribución original es la de la nueva partición en «1» y «2 o 3» más la distribución de «2 o 3» pero sólo cuando esa toque, que es la mitad de las veces, es decir
$latex H(\frac{1}{2},\frac{1}{3},\frac{1}{6})=H(\frac{1}{2},\frac{1}{2})+\frac{1}{2}H(\frac{2}{3},\frac{2}{3})$
Resulta ser que estas tres propiedades son suficientes para determinar que $latex H$ es
$latex H(p(i))=\sum_{i=1}^{n} p(i)\log{\frac{1}{p(i)}}$
Esto es igual de intuitivo quizás, pero el lector no acostumbrado a matemáticas no podrá seguir con tanta facilidad la demostración (que la puede ver en el apéndice de «A mathematical theory of communcation» – C. Shannon, 1948) luego se lo creería un poco a base de fe. El camino del artículo sí que es más fácil de seguir.
Otro punto interesante pero no comentado en el texto principal: ¿por qué escoger eventos de probabilidad 50% – 50%? ¿Qué ocurriría sino? Lo más sencillo es volver a la imagen del cuadrado que vamos partiendo por la mitad, y partirlo cada vez en, por ejemplo, cuatro zonas. Si el lector hace esto a mano se puede convencer de que en promedio vamos a necesitar preguntar muchas más veces para llegar a conocer el estado del sistema que en el caso de preguntas binarias. Por lo tanto al escoger particiones 50%-50% estamos hallando el mínimo número de preguntas necesarias para representar el sistema, luego es una cuestión de eficiencia.
