¿Te has preguntado alguna vez como se mueven las bacterias y los seres microscópicos? Lo más natural y lógico es pensar que nadando (empujar el agua y deslijarnos sobre él), pero eso, muy sorprendentemente, no es el caso. En este artículo explicaremos por qué nadar no funciona y, sin meternos en fórmulas, un mecanismo mediante el cual sí que pueden desplazarse.

Cuando con la mano intentas frotar un objeto, sientes una fuerza de fricción que se opone al movimiento. De manera análoga, cuando un trozo pequeño de fluido se mueve relativo a otro, hay fricción entre los dos elementos de fluido. También hay fricción entre el fluido y las paredes del contenedor o algún objeto sumergido dentro (como una bacteria).

Para cuantificar mejor la importancia de la fricción se utiliza el número de Reynolds que se puede definir como la relación entre las fuerzas de inercia (el término $latex ma$ en las ecuaciones de Newton) y las fuerzas de fricción.

$latex R\equiv \frac{\text{fuerzas inerciales}}{\text{fuerzas viscosas}} \approx \frac{av\rho}{\eta}$

donde $latex R$ es el número de Reynolds, $latex a$ es una longitud característica del objeto, $latex \rho$ es la densidad del fluido y $latex \eta$ es su viscosidad. No es de interés aquí demostrar la fórmula como tal porque no la vamos a usar.

¿Qué es la “fuerza de inercia” y la “fuerza de fricción”? Se refieren simplememente al término de segundo orden (aceleración) y el de primer orden (velocidad) en la ecuación del movimiento. Cuando el número de Reynolds es muy bajo, dominan las fuerzas de fricción sobre las de inercia y viceversa.

Ejemplo del muelle sobreamortiguado

Para concretar más, analizamos el caso sencillo de un muelle sobreamortiguado. ¿Por qué? Aunque un fluido no viene regido por estas ecuaciones sino por las de Navier-Stokes, podemos concretar más utilizando este ejemplo qué son las fuerzas de “inercia” (un poco mal-denominada así) y de fricción. Lo importante de esto es ver cómo la viscosidad hace que una de ellas sea más o menos importante (más concretamente, ver que para viscosidades altes el término de inercia se vuelve despreciable).

Recordando, este ejemplo trata de una masa puntual sujeta por un muelle clásico y todo el sistema inmerso en un fluido bastante viscoso. La fuerza viscosa suponemos que es proporcional a la velocidad. La ecuación de movimiento será pues:

$latex m\ddot{x}=-\gamma \dot{x}-k{x}$

donde $latex m$ es la masa, $latex x$ la posición, $latex k$ es la constante recuperadora del muelle, $latex \gamma$ es la viscosidad y un punto encima denota una derivada temporal.

La solución para el caso sobreamortiguado ($latex \gamma$ alto), es

$latex x=A e^{-\frac{k}{\gamma}t} + Be^{-\frac{\gamma}{m}t}$

donde $latex A$, $latex B$ son constantes que dependen de las condiciones iniciales. No demostraremos esto porque está hecho en muchos sitios (ver Referencias).

Para $latex \gamma$ muy alto, el segundo término desaparece porque la exponencial decae muy rápidamente y nos quedamos con $latex x=A e^{-\frac{k}{\gamma}t}$. La velocidad y aceleración se puede calcular derivando

$latex v = -\frac{k}{\gamma} x \rightarrow \text{fricci\’on} = \gamma v = -kx  $

$latex a= \frac{k^2}{\gamma^2} x \rightarrow \text{inercia} = ma=  \frac{mk^2}{\gamma^2} x $

Si $latex \gamma$ es muy grande, entonces el término de la aceleración es despreciable frente al de la velocidad. ¿Ves por qué?

¿Cuál es la consecuencia de todo esto? Esencialmente, en la ecuación del movimiento podemos ignorar el termino $latex m\ddot{x}$ y nos quedamos únicamente con una ecuación de primer orden: es decir, con conocer la posición inicial es suficiente para conocer la evolución de la partícula. La intuición detrás de lo último viene a ser la siguiente: cualquier velocidad inicial que tenga la partícula viene amortiguada casi instantáneamente por el medio viscoso y lo único que acaba importando es su posición. Este es un mundo aristotélico: cuando empujas algo se mueve y hay velocidad, pero cuando dejas de hacerlo se para. Además, si haces justo el movimiento opuesto y “vuelves sobre tus pasos” la velocidad tiene un sentido opuesto, luego la fuerza de fricción que sufre el cuerpo es opuesta también.

En el otro límite, cuando la viscosidad es más despreciable, recuperamos el término de la inercia en las leyes de Newton y las cosas vuelven a la normalidad. Para fluidos, el que el fluido no esté tan “adherido” consigo mismo hace más fácil la aparición de turbulencias y otros fenómenos sobre el cual el autor no está capacitado para hablar.

Que el lector mantenga en cuenta que el ejemplo del muelle es una analogía con el caso de los fluidos. Una diferencia muy importante es que para los fluidos el número de Reynolds, que nos da la importancia de las fuerzas viscosas sobre las inerciales, depende de la velocidad, entre otras cosas. Si uno se mueve muy lentamente en agua, ésta se comporta como un medio viscoso (como nadar en miel) pero si la velocidad es alta, no.

En el caso de las bacterias, se estima el número de Reynolds y se ve que es muy pequeño, por lo tanto éstas viven en un mundo sobre amortiguado. Ellas no pueden nadar como hacemos nosotros: movemos el cuerpo para empujar el agua y ganar inercia (en cierto sentido estamos deslizando sobre el agua), pero en el régimen sobre amortiguado el agua nos frena instantáneamente casi, luego no podemos usar dicho método.

Por lo tanto las bacterias necesitan hacer una fuerza continua para conseguir moverse (si hay fuerza se mueven, sino no). ¿Cómo pueden realizarla? Una primera idea sería unas aletas rígidas sencillas que tienen un movimiento periódico tal que para volver al punto inicial, recorra el mismo camino pero en sentido contrario. El problema consiste en que al volver sobre la misma trayectoria pero al revés, todas las fuerzas de rozamiento tienen un signo opuesto (porque la velocidad va en sentido contrario) luego acabas deshaciendo todo el progreso anterior. Para evitar esto debemos realizar movimiento cíclicos pero tal que al volver al punto incial lo hagamos por otro camino. Para que esto sea posible el sistema debe tener por lo menos dos grados de libertad (la aleta tiene sólo uno: el ángulo de la aleata rígida).

Una solución es el uso de un flagelo, que sería un sacacorchos que siempre gira en el mismo sentido en torno al eje de la hélice. Obviamente acabará volviendo al mismo punto de partido al ser el giro periódico, pero al no cambiar de sentido las fuerzas, no tomarán el signo opuesta y no desharemos todo el progreso ganado hasta ese momento.

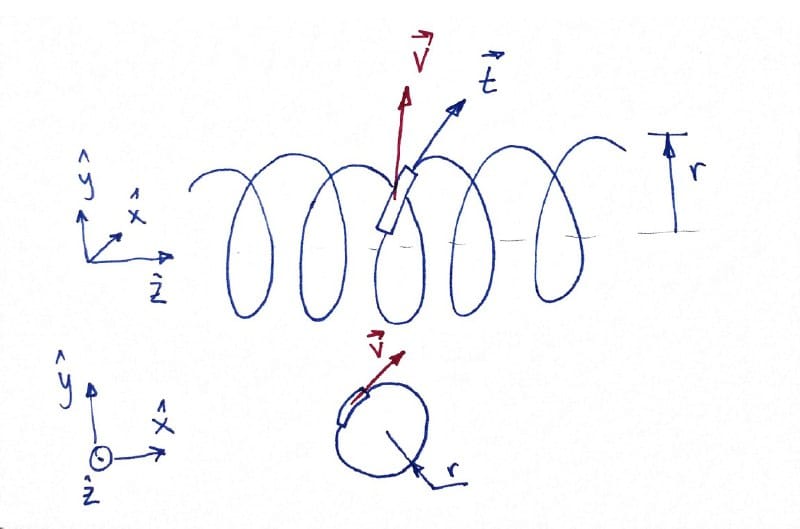
¿Por qué girar un sacacorchos en un medio viscoso causa una fuerza neta en su eje? Consideremos el siguiente experimento: si cogemos un trozo de cilindo y lo dejamos caer en miel orientado verticalmente, entonces caerá más rápidamente que orientado horizontalmente. Haciendo el experimento con cuidado se puede demostrar que la fuerza de fricción es mayor cuando el cilindro está orientado de una manera que de otra.

¿Y qué importancia tiene esto? Pues sorprendentemente, debido a ello si el cilindro no está en horizontal ni en vertical sino en diagonal, entonces se irá desplazando a un lado al ir cayendo por la gravedad. La clave del asunto es que al depender el coeficiente viscoso que nos da la fuerza de la dirección, la fuerza neta ya no es proporcional a la velocidad y por lo tanto no tiene que ser vertical. Al no ser vertical, tiene una componente horizontal que es lo que provoca el movimiento lateral del cilindro.

¿Esto cómo se aplica al flagelo? La hélice se puede descomponer en muchos cilindritos pequeños infinitesimales y al girar la hélice, el trocito de cilindro se mueve en el plano perpendicular al eje, como se puede ver en la siguiente figura. Entonces, la fuerza sobre el cilindro no será proporcional a la velocidad sino que tendrá una componente fuera, sobre el eje (análogo a como para el cilindro inclinado cayendo en miel la fuerza no es proporcional a la velocidad inicial vertical sino que está inclinada dando un desplazamiento horizontal).

Aunque no se entiendan todos los detalles, el punto clave es éste: usando que los coeficientes de fricción son distintos en la dirección paralela versus la perpendicular de un cilindro en un fluido viscoso y que una hélice se puede ver como suma de cilindritos pequeños, se consigue que al rotar la hélice/sacacorchos haya una fuerza neta y pueda haber propulsión de la bacteria.

Conclusiones

Como un breve repaso, hemos visto que el mundo microscópido es aristotélico: las cosas se mueven solo cuando haces fuerzas sobre ellas. Para que se desplacen las bacterias no pueden darse impulsos y dejarse mover por la inercia sino que deben hacer una fuerza continua. Un ejemplo de propulsor sería un flageo o hélice giratoria que, usando el hecho de que la fricción es distinta cuando el movimiento es perpendicular versus paralelo a la superficie del flagelo, puede crear una fuerza neta distinta de cero en la dirección de su eje principal y de esta manera propulsar la bacteria.

Referencias

E. M. Purcell, “Life at low Reynolds number”, American journal of physics 45, 3 (1977).

Para la solución del oscilador harmónico sobreamortiguado: Solución al oscilador armónico.